In den Umkleideräumen eines Schwimmbades stehen 100 Personen. Die erste Person öffnet alle Spinde. Die zweite öffnet jeden zweiten Spind. Die dritte ändert den Zustand jedes dritten Spindes, d.h. der Spinde 3, 6, 9 usw. trifft sie auf einen offenen Spind, so verschließt er diesen, trifft er auf einen verschlossenen Spind, so öffnet sie ihn. Die Frage lautet nun: Welche Spinde sind am Ende, wenn alle 100 Personen die Umkleideräume passiert haben, noch offen?
Wir werden diese Fragestellung, wie auch die zuvor schon behandelten Probleme zunächst im klassischen Programmierstil mit Mathematica lösen.Danach werden wir eine Lösung angeben, die mit "Mathematica-Bordmittlen" erzeugt ist und wesentlich näher "am Problem" ist.
Die klassische Herangehensweise
Wir betrachten hier ein Problem, daß als "Locker-Problem" in der Informatik bekannt ist. Es geht dabei um folgendes:
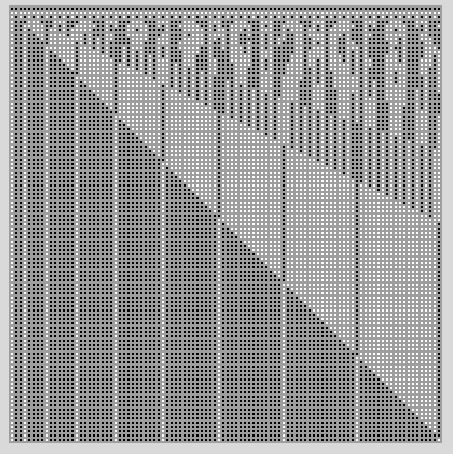
In den Umkleiderräumen eines Schwimmbades stehen 100 Studenten. Der erste Student verschließt alle Spinde. Der zweite Student öffnet jeden zweiten Spind. Der dritte Student ändert den Zustand jedes dritten Spindes, d.h. der Spinde 3, 6, 9 usw. trifft er auf einen offenen Spind, so verschließt er diesen, trifft er auf einen verschlossenene Spind, so öffnet er ihn. Die Frage lautet nun: Welche Spinde sind am Ende, wenn alle 100 Studenten die Umkleideräume passiert haben, noch offen?
Wir werden diese Fragestellung, wie auch die zuvor schon behandelten Probleme zunächt im klassichen Programmierstil mit Mathematica lösen. Die Lösung ist hier kein größeres Problem. Die Lösung läßt sich mit zwei geschachtelten Schleifen einfach ermitteln. Der Einfachheit halber beginnen wir erst mit dem zweiten Studenten und der Ausgangssituation, daß alle Spinde offen sind.
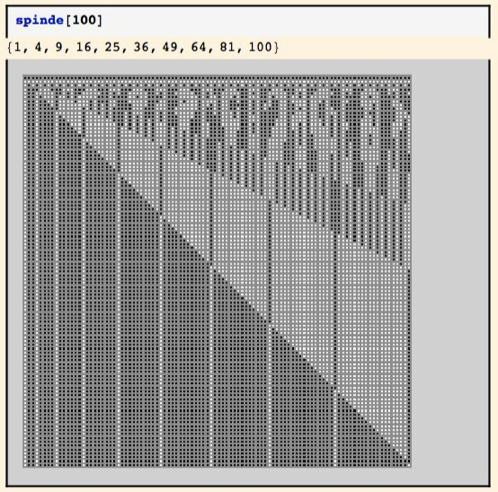
Es bleiben also alle Spinde offen deren Nummern Quadratzahlen sind. Ein durchaus nicht offensichtliches Ergebnis.
Die Mathematica Herangehensweise
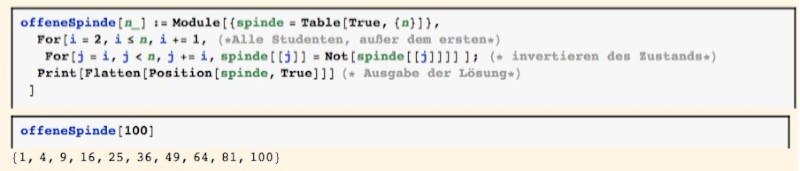
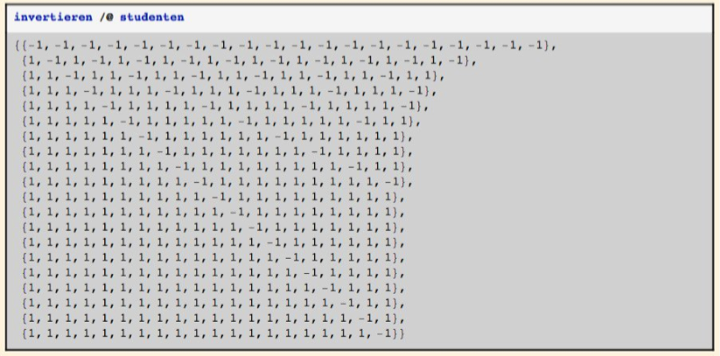
Nun soll auch dieses Problem wieder im Mathematica Stil angegangen und gelöst werden. Die Grundidee ist dabei die offenen Spinde als Liste von Zahlen zu repräsentieren. Dabei steht +1 für einen offenen Spind und -1 für einen verschlossenen Spind. DieseWahl der Darstellung ermöglicht es die Invertierung des jeweiligen Spindzustandes durch eine Multiplikation mit -1 zu realisieren. Dies wiederum ermöglicht es die zugrundeliegende Iteration mit Hilfe der Mathematica-eigenen Iterationsfunktionen (hier FoldList) zu implementieren. Betrachten wir die Vorgehensweise etwas genauer, indem wir das Problem Schritt für Schritt lösen. Wir betrachten dabei anzahl Spinde. Zunächst die Spinde, dann die Studenten:







Download
Mathematica Notebook
PDF
